Subglacial hydrology from high-resolution ice-flow simulations of the Rhine Glacier during the Last Glacial Maximum: a proxy for glacial erosion

At the Last Glacial Maximum (LGM), the Rhine Glacier complex (Rhine and Linth glaciers) formed large piedmont lobes extending north into the Swiss and German Alpine forelands. Numerous overdeepened valleys there were formed by repeated glaciations. A characteristic of these overdeepened valleys is their location close to the LGM ice margin, away from the Alps. Numerical models of ice flow of the Rhine Glacier indicate a poor fit between the sliding distance, a proxy for glacial erosion, and the location of these overdeepenings. Calculations of the hydraulic potential based on the computed time-dependent ice surface elevations of the Rhine Glacier lobe obtained from a high-resolution thermo-mechanically coupled Stokes flow model are used to estimate the location of subglacial water drainage routes. Results indicate that the subglacial water discharge is high and focused along glacial valleys and overdeepenings when water pressure is equal to the ice overburden pressure. These conditions are necessary for subglacial water to remove basal sediments, expose fresh bedrock, and favor further erosion by quarrying and abrasion. Knowledge of the location of paleo-subglacial water drainage routes may be useful to understand patterns of subglacial erosion beneath paleo-ice masses that do not otherwise relate to the sliding of ice. Comparison of the erosion pattern from subglacial meltwater with those from quarrying and abrasion shows the importance of subglacial water flow in the formation of distal overdeepenings in the Swiss lowlands.

1 Introduction

At the Last Glacial Maximum (LGM), the Rhine Glacier complex (Cohen et al., 2018), combining the Rhine and Linth glaciers, descended well into the Swiss and German Alpine forelands, forming two large piedmont lobes. The Rhine Glacier lobe covered present-day Lake Constance and land to the north in southern Germany, and the Linth Glacier lobe advanced beyond the city of Zurich, Switzerland. Repeated glaciations since the Middle–Late Pleistocene (Preusser et al., 2011; Ellwanger et al., 2011) have carved numerous landforms in the Alps such as deep alpine valleys with prominent horns and ridges. In the forelands, the passage of glaciers left numerous imprints on the landscape such as terminal moraines, outwash deposits, and erratics (e.g., Schlüchter, 1988, 2004; Keller and Krayss, 2005a; Preusser et al., 2007; Beckenbach et al., 2014; Gaar et al., 2019); drumlin fields (Kamleitner, 2022); tunnel valleys (Reber and Schlunegger, 2016); and overdeepened valleys now filled with sediments such as the Thur, the Glatt, and the Aare valleys (e.g., Preusser et al., 2011; Dehnert et al., 2012; Dürst Stucki and Schlunegger, 2013) or with water such as Lake Constance and Lake Zurich. A surprising characteristic of these overdeepenings along these valleys is their proximity to the terminal position of past glacial maxima in a region where one would expect that the erosive power of ice, often associated with the rate of sliding at the base (e.g., Hallet, 1981; Humphrey and Raymond, 1994; MacGregor et al., 2000; Koppes et al., 2015; Herman et al., 2015), would be smaller in comparison to that of large alpine valleys where ice fluxes and sliding speeds are higher. The existence of these overdeepenings in a distal-foreland setting thus remains puzzling.

Previous models of ice flow of the Rhine Glacier (Cohen and Jouvet, 2017; Haeberli et al., 2020; Fischer et al., 2021; Seguinot and Delaney, 2021) indicate that the sliding distance, a proxy for glacial erosion based on the time-integrated sliding speed, or a power of it, during the advance and retreat of the Rhine Glacier lobe into the foreland, does not correlate well with the location of existing overdeepenings (Fig. 1) owing to the short time period over which ice covered these distal forelands. More recent work by Egholm (2022) using a landscape evolution model indicates that the formation of distal overdeepenings is possible if the rock material is significantly weaker there than the material in the Alpine massif. The model of Egholm (2022) used empirical parametrizations of abrasion and quarrying (Ugelvig et al., 2018) that were fitted against theoretical models (Hallet, 1981; Iverson, 2012). Egholm (2022)'s results, however, were mostly obtained using a steady-state climate model in which ice occupation time over the Swiss Alpine foreland was artificially long, in contrast with the geomorphic record for the Rhine Glacier (e.g., Keller and Krayss, 2005b) that suggests a maximum extent lasting a couple of thousand of years. This dilemma begs the question as to what other subglacial glaciological process could have contributed to the erosion of the northern Alpine forelands and the formation of these distal overdeepenings.

Several authors have noted the importance of subglacial water in glacial erosion (see review by Alley et al., 2019). Erosion by quarrying (Hooke, 1981; Iverson, 1991; Alley et al., 1999), whereby blocks of rock are plucked from the glacier bed by the moving ice, depends on subglacial water pressure fluctuations. Field experiments (Cohen et al., 2006) and models of quarrying (Iverson, 1991, 2012; Hallet, 1996; Beaud et al., 2014; Ugelvig et al., 2018) have shown a link between fluctuations in water pressure and the rate of opening of pre-existing bedrock cracks and fractures. Furthermore, large-scale investigations of the erosive power of glaciers (Koppes et al., 2015) indicate that temperate basal conditions, which imply the presence of subglacial water, are indicative of higher erosion rates, particularly at middle to high latitudes where seasonal and diurnal temperature variations are high and thus increase the possibility of significant water pressure fluctuations. Subglacial water is also key to the removal of sediments eroded and deposited at the base of glaciers (e.g., Hallet, 1996) that would otherwise blanket the bedrock, preventing any erosion process from occurring (Alley et al., 2019). Indeed, freeze-on conditions along the adverse slope of overdeepenings inhibit subglacial water flow and sediment removal, leading to decrease in erosion there (e.g., Hooke, 1991; Alley et al., 2003; Werder, 2016). Thus, subglacial water plays an important role in the erosive power of glaciers.

Lacking a clear link between sliding ice (or motion) and observed locations of overdeepenings in the Swiss Alpine forelands underneath the paleo-Rhine Glacier and paleo-Linth Glacier lobes, we seek to find whether subglacial water drainage distribution under the paleo-Rhine Glacier complex could help us understand the location of these overdeepenings. Our approach uses the numerical ice-flow model described in Cohen et al. (2018) but with a new climate signal to drive the ice model and a finer horizontal discretization to better resolve the ice flow. Calculated ice surface elevation, together with basal topography, allows us to compute the hydraulic potential and hydraulic head and the associated flow accumulation area during the course of advance and retreat of the Rhine Glacier around the LGM. Time integration of the flow accumulation area yields a metric for glacial erosion by subglacial water to test against the positions of observed overdeepenings. The underlying assumption in this analysis is that larger values of the time-integrated flow accumulation area indicate zones with significant subglacial water flow, which, over seasonal and annual timescales, have high potential for subglacial water fluxes that would enhance sediment removal and increase glacial erosion. We then compare patterns of relative erosion by quarrying, abrasion, and subglacial water flow to show the importance of subglacial water in the formation of distal overdeepenings in the Swiss lowlands.

The remainder of this paper is divided into three parts. Section 2 presents the methodology to compute the time-integrated flow accumulation area and the erosion by quarrying, abrasion, and subglacial water; Sect. 3 discusses the source of the data used for the computation; finally, Sect. 4 reports results and discusses them.

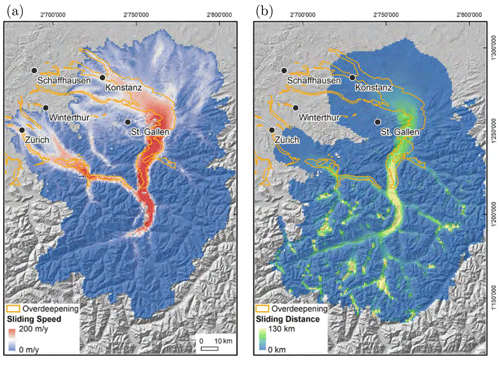
Figure 1 Map of (a) sliding speed and (b) sliding distance calculated by integrating the sliding speed over the advance and the retreat of the Rhine Glacier system during the last glacial cycle (see Cohen, 2017; Cohen and Jouvet, 2017; and Cohen et al., 2018, for details). The location of overdeepenings is indicated in orange. Reproduced from Fischer et al. (2021).

2 Methods

Subglacial water flow paths are calculated using the method described in Chu et al. (2016) (see also Arnold et al., 1998; Willis et al., 2012; Livingstone et al., 2013) and used in several studies to estimate subglacial water drainage locations in Greenland and Antarctica (e.g., Le Brocq et al., 2009; see also references in Chu et al., 2016) and in paleo-ice masses such as the Fennoscandian Ice Sheet (e.g., Shackleton et al., 2018). More sophisticated models of subglacial hydrology (e.g., GlaDS; Werder et al., 2013) coupled to ice-flow models (e.g., Gagliardini and Werder, 2018, with Elmer/Ice) are too computationally expensive to be applied to the long timescales and the large complex topography of the paleo-Rhine Glacier system.

Water flows down the hydraulic potential gradient, and the water flux, Q, can be calculated as (Shreve, 1972)

$$\begin{array}{}\text{(1)}& Q=-k\mathrm{\nabla }\mathit{\varphi },\end{array}$$

where k is the hydraulic conductivity of the subglacial water system and ϕ is the hydraulic potential, defined as

$$\begin{array}{}\text{(2)}& \mathit{\varphi }={\mathit{\rho }}_{\mathrm{w}}g{Z}_{\mathrm{b}}+p_{\mathrm{w}}.\end{array}$$

Here ρ_w=1000 kg m⁻³ is the density of water (constant), g=9.81 m s⁻² is the acceleration due to gravity, Z_b is the elevation of the basal surface (glacier bed topography), and p_w is the water pressure. In glaciological applications, the water pressure at the bottom of the ice is often not known. In paleo-glaciological applications, no subglacial water pressure data exist, so it is often not computed (e.g., Cohen et al., 2018). Here we assume that the water pressure at the bed of the glacier is a fraction of the ice overburden pressure; i.e.,

$$\begin{array}{}\text{(3)}& p_{\mathrm{w}}=f{p}_{\mathrm{i}},\end{array}$$

where f is known as the flotation factor and

$$\begin{array}{}\text{(4)}& p_{\mathrm{i}}={\mathit{\rho }}_{\mathrm{i}}gH,\end{array}$$

with ρ_i=917 kg m⁻³ being the ice density (constant) and H the ice thickness (variable). Substituting Eqs. (3) and (4) into Eq. (2) yields

$$\begin{array}{}\text{(5)}& \mathit{\varphi }={\mathit{\rho }}_{\mathrm{w}}g{Z}_{\mathrm{b}}+f{\mathit{\rho }}_{\mathrm{i}}gH,\end{array}$$

where the hydraulic potential now only depends on the basal surface topography and the ice thickness. As an alternative we can use the hydraulic head, h, defined as

$$\begin{array}{}\text{(6)}& h=Z_{\mathrm{b}}+f{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}}{{\mathit{\rho }}_{\mathrm{w}}}}H.\end{array}$$

The value of the flotation factor f depends on the basal water pressure. When water pressure equals ice overburden pressure, f=1. Values greater than 1 are observed during times of intense surface melt that bring water through crevasses and moulins directly to the bed of the glacier (Meierbachtol et al., 2013; Wright et al., 2016). Since our ice-flow model (Cohen et al., 2018) does not simulate subglacial water pressures and given the uncertainties in both the basal surface during the last glacial cycle and estimates of the ice surface, we assume spatially fixed values of f over the entire glacier system and compute the hydraulic potential for three cases – f=0.6, f=1, and f=1.1 – to study the effects of water pressure on subglacial water drainage paths. Low values of f imply that basal topography dominates, while higher values emphasize the ice surface topography (see Eq. 6).

The subglacial water drainage paths can be obtained by computing the upstream accumulation area at each of the cells of the raster of the hydraulic head (Flowers and Clarke, 1999; Fischer et al., 2005; Chu et al., 2016; Pitcher et al., 2016) using the D_∞ algorithm of Tarboton (1997) to compute flow directions. Water drainage flow paths are continuous paths with high values of upstream accumulation areas.

On the long timescales over which erosion occurs (on the order of thousands of years), the ice thickness (H in Eq. 6) evolves with advances and retreats of the glacier. To include these transient effects, we compute the subglacial water flow paths at each available time step for the ice surface (every 10 years) and integrate the computed upstream accumulation area over time to obtain a time-integrated view of subglacial water drainage paths.

Estimates of erosion by subglacial water flow are calculated using the method of Kirkham et al. (2022) based on a model of subglacial channel erosion by Carter et al. (2017). Here we only compute the erosive component (see Kirkham et al., 2022, Eq. 3),

$$\begin{array}{}\text{(7)}& {\dot{E}}_{\mathrm{s}}=K_{\mathrm{1}}\left({\displaystyle \frac{{\mathit{\nu }}_{\mathrm{s}}}{{\mathit{\alpha }}_{\mathrm{cc}}}}\right){\left({\displaystyle \frac{\max \left({\mathit{\tau }}_{\mathrm{cc}}-{\mathit{\tau }}_k,\mathrm{0}\right)}{g\left({\mathit{\rho }}_{\mathrm{s}}-{\mathit{\rho }}_{\mathrm{w}}\right)D_{\mathrm{15}}}}\right)}^{\mathrm{3}/\mathrm{2}},\end{array}$$

where

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{cc}}=\mathrm{0.125}{f}_{\mathrm{cc}}{\mathit{\rho }}_{\mathrm{w}}{u}_{\mathrm{c}}^{\mathrm{2}},\text{(9)}& {\displaystyle }{\mathit{\tau }}_k=\mathrm{0.025}{D}_{\mathrm{15}}g({\mathit{\rho }}_{\mathrm{s}}-{\mathit{\rho }}_{\mathrm{w}}),\text{(10)}& {\displaystyle }{\mathit{\nu }}_{\mathrm{s}}=D_{\mathrm{15}}^{\mathrm{2}}{\displaystyle \frac{({\mathit{\rho }}_{\mathrm{s}}-{\mathit{\rho }}_{\mathrm{w}})g}{\mathrm{9}{\mathit{\mu }}_{\mathrm{w}}}}.\end{array}$$

Here τ_cc is the channel shear stress, τ_k is the critical shear stress, ν_s is the mean sediment velocity, u_c is the water velocity in the channel, f_cc=0.07 m${}^{-\mathrm{2}/\mathrm{3}}$ s⁻² denotes the channel roughness parameters, ρ_s=2600 kg m⁻³ is the solid density of sediment grains, D₁₅=0.1 mm is the 15th-percentile grain size, and ${\mathit{\mu }}_{\mathrm{w}}=\mathrm{1.78}\times {\mathrm{10}}^{-\mathrm{3}}$ Pa s is the viscosity of water. The water flow velocity in the channel, u_c, is computed from the flow accumulation area weighted by the available meltwater at each cell, which is estimated by summing the surface melt rate and the basal melt rate. The meltwater is then scaled by multiplying it by the grid cell area divided by the cross-sectional area of the channel, assumed to be 30 m wide and 2 m deep, to obtain the channel water velocity. Although changing the channel size would affect the relationship between τ_cc and τ_k and thus where erosion occurs, it does not affect the overall results of erosion patterns as our calculations are meant to only look at erosion patterns and not calculate erosion magnitudes. The surface melt rate is calculated in the ablation area of the glacier and is proportional to the number of positive degree days (PDDs) (Hock, 2003). It is assumed to be zero in the accumulation area. The basal melt rate is computed from the geothermal heat flux map of Medici and Rybach (1995). Frictional heat generated by ice sliding over the substrate is an order of magnitude smaller than either surface or basal melt and is thus neglected.

To compare patterns of subglacial erosion due to ice motion, we also estimate erosion by quarrying, ${\dot{E}}_{\mathrm{q}}$, and abrasion, ${\dot{E}}_{\mathrm{a}}$, given, respectively, by (see Ugelvig et al., 2016, 2018)

$$\begin{array}{}\text{(11)}& {\displaystyle }{\dot{E}}_{\mathrm{q}}=K_{\mathrm{q}}{p}_{\mathrm{e}}^{\mathrm{3}}{v}_{\mathrm{s}},\text{(12)}& {\displaystyle }{\dot{E}}_{\mathrm{a}}=K_{\mathrm{a}}{v}_{\mathrm{s}}^{\mathrm{2}},\end{array}$$

where $p_{\mathrm{e}}=p_{\mathrm{w}}-p_{\mathrm{i}}$ is the effective pressure, v_s is the glacier sliding speed, and K_q and K_a are constants.

All erosion rates are time-integrated to yield a total erosion over the course of the advance and retreat of the glacier during the LGM. Because of uncertainties in model and parameter values, a direct comparison between quarrying, abrasion, and subglacial meltwater erosion is not possible. Instead, these quantities are used to look at relative patterns of erosion by normalizing them. This makes the exact values of the parameters K₁ (Eq. 7) and K_q and K_a (Eqs. 11 and 12, respectively) irrelevant.

3 Data

Only two surfaces are required to compute the hydraulic potential and subglacial water flow paths: the basal surface (Z_b in Eq. 6) and the ice surface from which the ice thickness, H, can be obtained (see Eq. 6). The ice surface is computed from ice-flow simulations of the paleo-Rhine Glacier complex around the LGM using Elmer/Ice, an open-source, finite-element multi-physics Fortran code (Gagliardini et al., 2013; Ruokolainen et al., 2020). Elmer/Ice computes the transient three-dimensional ice velocities, temperatures, and pressures as well as the elevation of the ice surface based on fully coupled thermo-mechanical equations by solving the non-linear Stokes flow equation together with the heat equation and the mass balance equation at the ice surface (see Cohen et al., 2018, for details). The mass balance is based on the positive-degree-day model (Hock, 2003) that computes ice melt as a function of air temperature. PDDs are computed using the method of Calov and Greve (2005) over month-long intervals using factors of 8 and 3 mm ^∘C⁻¹ d⁻¹ for ice and snow, respectively. Air temperature and precipitation are obtained by linear interpolation using a glacial-index (GI) approach (Sutter et al., 2019) between LGM and pre-industrial (PI) climate states. The GI follows the δ¹⁸O signal of the Antarctica EPICA ice core (Jouzel et al., 2007), rescaled to between 0 (no ice, PI) and 1 (maximum ice volume at the LGM). The LGM climate state provides 2 km resolution maps of the temperature and precipitation over the entire Alps computed from a regional climate model by dynamical downscaling of a global Earth system model (see details in Velasquez et al., 2020, 2022; Russo et al., 2022; Buzan et al., 2023).

3.1 Basal surface

The basal surface is the present-day topography minus the computed ice thickness of major present-day glaciers using the model of Farinotti et al. (2019). It remains unchanged during the ice-flow simulation. Figure 2 shows the basal topography used in the model simulation.

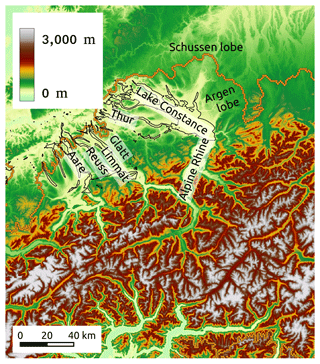
Figure 2 Basal topography with outline of overdeepened basins in black and extent of ice at the LGM with orange circles (Ehlers and Gibbard, 2008).​​​​​​​

3.2 Ice surface

The ice surface evolves with time during the advance of the Rhine Glacier towards its maximum LGM position and during its retreat. Figure 3 shows three ice surface elevations at 27 ka, at 22.9 ka (LGM), and at 14.2 ka. Ice surface elevations are available every 10 years from 27 to 14.2 ka.

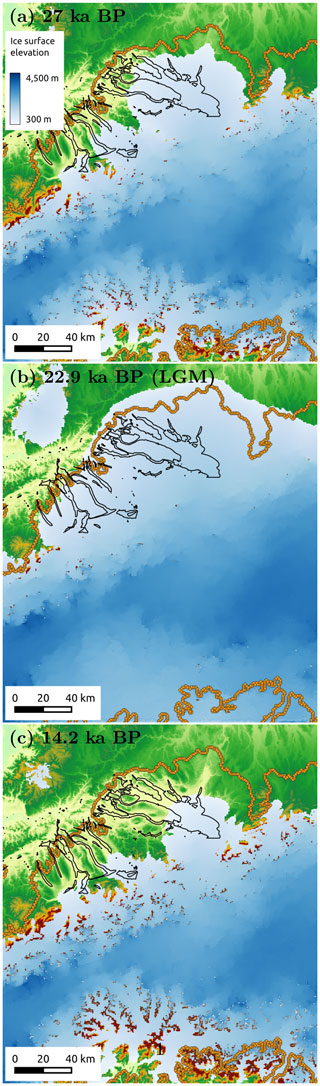
Figure 3 Ice surface elevation in blue at (a) 27 ka (start of simulation), (b) 22.9 ka (LGM), and (c) 14.2 ka (end of simulation). LGM ice extent is shown with orange circles (Ehlers and Gibbard, 2008).

3.3 Calculation of hydraulic potential and flow accumulation area

The hydraulic potential is first calculated on the unstructured triangular mesh of the Elmer/Ice finite-element model at every time step (every 10 years). Resolution in the mesh ranges from 800 to 1100 m, with increased resolution in areas of steeper slope gradients. The nodal values of the hydraulic potential are then linearly interpolated to a uniform raster at a resolution of 500 m. The calculation of the flow accumulation area is performed on the hydraulic potential using the open toolbox SAGA (System for Automated Geoscientific Analyses; Conrad et al., 2015) and summed over time to compute the time-integrated values.

4 Results and discussion

Figure 4 shows the subglacial water drainage routes based on the flow accumulation area of the hydraulic potential (or hydraulic head) at three different times for flotation values of f=0.6 (Fig. 4, left panels), f=1.0 (Fig. 4, center panels), and f=1.1 (Fig. 4, right panels).

Figure 4 The log ₁₀ of computed flow accumulation area (in m²) in blue at three different times – (a, b, c) 27 ka, (d, e, f) 22.9 ka (LGM), and (g, h, i) 14.2 ka – based on the hydraulic potential for a flotation factor of (a, d, g) f=0.6, (b, e, h) f=1.0, and (c, f, i) f=1.1. Hillshade topography and ice thickness in red shades at the times indicated are shown in the background. Actual LGM ice extent is shown with orange circles. Modeled ice extent is shown with a brown line. Black outlines indicate locations of overdeepenings.

The flow accumulation area can be understood as a proxy for subglacial water flux that passes through a specific drainage channel because water flux to the glacier is an increasing function of the upstream flow accumulation area.

When f=0.6 (Fig. 4, left panels), subglacial water drainages are mostly concentrated in the Alpine Rhein Valley in the Alps, in Lake Constance, and along major valleys in the forelands such as the drainage of Lake Zurich. Drainages are constrained by basal topography, following valley morphology. Lake Constance (a zone of constant elevation), where the Alpine Rhein Glacier flows, concentrates a significant flux of subglacial water according to the model. Water exits the Rhine Glacier lobe to the north via existing valleys in the German Alpine foreland, following the Überlingen branch of present-day Lake Constance. In the Swiss Alpine foreland, water drains out of Lake Constance via the Untersee and also by connecting to the Thur Valley, which coincides with an overdeepening there. In the Linth Glacier lobe, subglacial water also flows along Lake Zurich and the Limmat and Glatt valleys, where two overdeepenings are located (Preusser et al., 2010; Buechi et al., 2018). The Reuss and Aare overdeepenings are also pathways for subglacial water drainages further to the west. The drainage pattern does not change significantly with time (see Fig. 4a, c, e) except at t=14.2 ka when the ice has retreated halfway out of Lake Constance and completely out of the distal overdeepenings in the Swiss forelands.

The drainage pattern is significantly different when f=1.0 (Fig. 4, center panels), equivalent to zero effective pressure at the base. Water now drains out of the Lake Constance basin to the north in many concentrated flow channels, such as the Schussen Valley, against an adverse bedrock slope (see basal topography in Fig. 2) and where a few overdeepenings have been noted (Ellwanger et al., 2011). Subglacial flow is also more important along many valleys in the foreland, both in the Rhine Glacier (e.g., Thur) and in the Linth Glacier (e.g., Reuss) lobes. Because of higher water pressure, the hydraulic potential gradient conforms less to the basal (or bed) topography, and subglacial water moves more along the gradient determined by the slope of the glacier surface; subglacial water paths no longer follow topographic lows.

At a yet higher flotation value (f=1.1, Fig. 4, right panels), when water pressure exceeds ice overburden pressure, subglacial drainages out of the Alpine Rhine are also diverted to the north across Lake Constance and then ascending the bedrock slope north of it. Water drainage, however, occurs over many more subglacial channels that fan out radially from the Lake Constance basin. Because of the high water pressures, drainages are no longer constrained by basal topography and can move from one valley to the next over topographic high points such as from the Thur to the Lower Rhine overdeepenings out of the Untersee. High flotation values cause water drainage paths to cut across valleys and overdeepenings, such as, for example, in the Thur Valley, in the Rhine Glacier lobe, and in the Reuss and Linth lobes. In the Alps, water drainage paths are no longer constrained to the valley centers but meander on the sides of the valley and along the valley walls (contrast Fig. 4d and f), even cutting across mountain ranges during retreat (see Fig. 4i).

Basal conditions where the value of flotation is equal to 1 or greater are unlikely to occur over the entire glacier basal surface and for significant lengths of time. High basal water pressure arising from increased surface melting would promote the development of an efficient drainage system that would tend to reduce basal water pressure (e.g., Bartholomaus et al., 2008; Sundal et al., 2011; Andrews et al., 2014). These basal conditions, despite their limited duration, could have the potential to produce significant changes in the basal geomorphology, for example, because of substantial increases in the capacity of subglacial water streams to transport sediments and in their ability to further erode bedrock by processes of abrasion and quarrying associated with both larger fluctuations in basal water pressure and increased basal sliding speed (e.g., van de Wal et al., 2008; Schoof, 2010; Bartholomew et al., 2010; Hewitt, 2013).

The time integration of subglacial water flow paths over the 12.8 kyr of the simulation covering advance and retreat of the Rhine Glacier around the LGM is shown in Fig. 5 for the three values of flotation: f=0.6, 1, and 1.1.

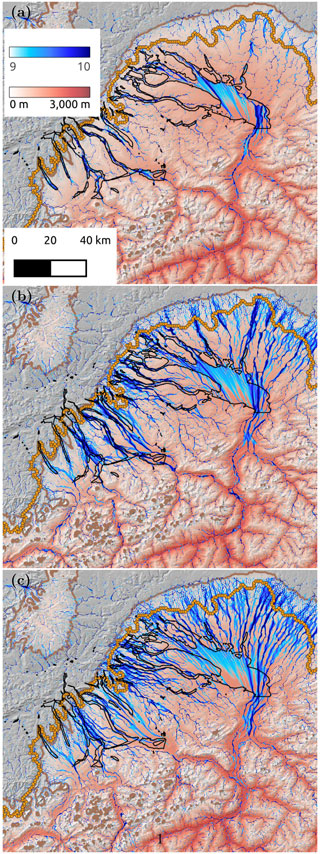
Figure 5 The log ₁₀ of the time-integrated flow accumulation area (in m²) over 12.8 kyr (in blue) for (a) f=0.6, (b) f=1, and f=1.1 with hillshade topography and ice thickness at the LGM (red colors) in the background. LGM ice extent is shown with orange circles. Model ice extent is shown with a brown line. Black outlines indicate location of overdeepenings.

Clear differences exist between a moderate flotation value (f=0.6) and flotation values with zero effective pressure (f=1) or where water pressure exceeds ice overburden pressure (f=1.1). Although high water pressures in excess of hydrostatic pressure have been noted in both Alpine (e.g., Flowers and Clarke, 1999) and Greenland (e.g., Banwell et al., 2013; Lindbäck et al., 2015) settings and may be occurring in overdeepenings (Lawson et al., 1998), they may not be representative of long-timescale average values in large areas of the Rhine Glacier lobe. Subglacial water flow drainages with high water pressure bypass some topographic relief, producing near-straight channels that cut across relief, such as in the northern part of the Rhine Glacier lobe. These high-water-pressure subglacial drainage paths also cut across overdeepenings in the Thur, Glatt, and Limmat overdeepenings in the Rhine Glacier and Linth Glacier lobes. A value of f equal to unity yields the closest match with the actual mapping of overdeepenings, although many overdeepenings are also well matched for f=0.6, particularly in the Linth Glacier lobe and the lower Thur Valley. Overdeepened regions north of Lake Constance require higher flotation values to be occupied by a subglacial water drainage path. When water pressure exceeds ice overburden pressure such as when f=1.1, subglacial drainages are too distributed and no longer only conform to valleys, a situation that may occur during periods of significant melt (such as during retreat) but is likely not representative of the situation over longer timescales.

High values of the time-integrated flow accumulation area represent drainage pathways with large fluxes of water. Many of these high-discharge zones correspond to several locations of overdeepenings such as the Schussen, Thur, Limmat, Reuss, and Aare overdeepened valleys. In the Aare Valley, a tunnel valley system has been identified beneath the city of Bern (Dürst Stucki and Schlunegger, 2013; Reber and Schlunegger, 2016) with a branching pattern that resembles the pattern observed in our simulation. The presence of this tunnel valley system has been associated with an area of high water pressure. Our simulation also indicates that a flotation value of 1 is necessary for significant subglacial water drainage to occur in this area.

Figure 6 shows patterns of erosion for quarrying, abrasion, and subglacial water flow. All values of erosion have been scaled to between 0 and 1 by dividing the computed values by their respective maximum value. All erosion types have been time-integrated over the course of the advance and retreat of the ice during the LGM.

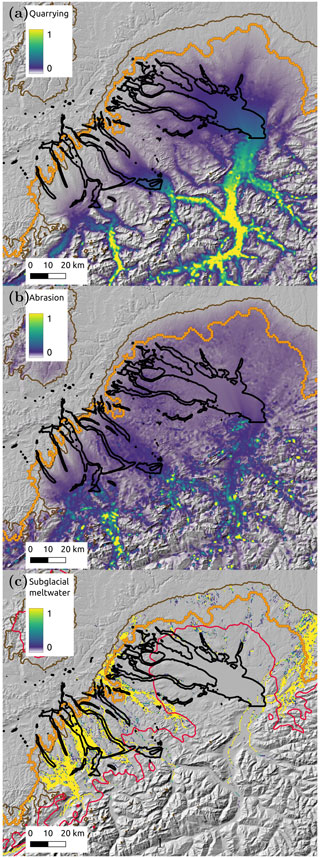
Figure 6 Normalized erosion by (a) quarrying, (b) abrasion, and (c) subglacial meltwater flow. Background shows hillshade topography. LGM margin is shown with orange circles; modeled maximum LGM extent is shown with a brown curve. Black curves indicate areas of overdeepenings. The red curve in (c) is the equilibrium line at the LGM separating accumulation (south) from ablation (north) in the Alps.

A clear difference in the erosion pattern emerges between erosion due to ice motion (quarrying and abrasion) and erosion due to subglacial meltwater flow. Erosion by ice motion is greatest at the base of alpine valleys where sliding is fastest and where the ice occupation time is longest. Limited durations of ice cover and lower sliding speeds near the margin limit erosion by ice motion there. Erosion by quarrying (Fig. 6a) shows more variability in the Rhine, Linth, and Reuss lobes owing to its cubic dependence on the ice thickness via the effective pressure term (see Eq. 11). Any variation in ice thickness along or across overdeepenings amplifies erosion by quarrying, resulting in a significant change in the total amount of quarrying in these areas. In contrast, erosion by abrasion (Fig. 6b), which only depends on the square of the sliding speed (see Eq. 11), is more uniform in these lobes. Erosion by subglacial meltwater flow (Fig. 6c) is significantly different: it is almost entirely focused near the ice margin, particularly to the northwest in the Reuss and Linth lobes, the Thur Valley, and the Argen lobe (see Fig. 2). This is due to the large available surface melt in these areas that have larger ablation areas. This is visible by comparing, for example, the position of the equilibrium line (Fig. 6c, red line) to the LGM margin (Fig. 6c, brown line). In the northwestern lobes and in the northeastern part of the Rhine lobe, the area for available surface meltwater is significantly larger then in the main Rhine lobe, explaining why most erosion by subglacial meltwater occurs preferentially there. Also, channel shear stress is more likely to exceed critical shear stress in areas where subglacial channel velocity is higher (see u_c in Eq. 8), which occurs where more surface melt is available and thus increases the potential for erosion by subglacial meltwater.

The different erosion patterns due to ice motion and subglacial meltwater suggest that the existence of distal-foreland overdeepenings in the Swiss lowlands is driven, at least in part, by erosion by subglacial meltwater. Furthermore, high water flux during high-water-pressure events along these valleys and the associated fluctuations in water pressure in the channels could have increased the rate of glacial erosion by quarrying (e.g., Cohen et al., 2006), a dependence that is not included in the simple quarrying erosion law in Eq. (11). This may have been further enhanced by pre-existing rock weaknesses due, for example, to a higher density of joints or faulting (e.g., Dühnforth et al., 2010; Hooyer et al., 2012) such as is found in the Lake Constance area (Fabbri et al., 2021). The patterns of subglacial water drainage paths computed from numerical simulations of ice flow and ice surface elevation indicate a possible link between the subglacial water flux and the existence of overdeepenings. The location of these overdeepenings suggests that these overdeepenings are controlled, in part, by higher rock erodibility in these areas, which, during glacial times, were preferentially excavated by the combined effects of water and ice.

5 Conclusions

We present a model of subglacial water drainages underneath the Rhine Glacier during the advance and retreat around the LGM. The model is based on high-resolution ice surfaces obtained from a numerical ice-flow model. The model computes ice velocities and ice surface elevations using a thermo-mechanical Stokes flow model coupled to a high-resolution regional climate model to give the most plausible representation of the Rhine Glacier during its advance and retreat around the LGM. The hydraulic potential (or head) calculated from transient elevations of the ice surface together with the basal topography yields a map of subglacial water flux during the LGM. Results of the calculation show that subglacial water drainage is strongly constrained by topography for low values of water pressure (small flotation factor), focusing water flow in valleys in the foreland. When water pressure equals ice overburden pressure (flotation value equal to 1), the subglacial drainages coincide with regions of intense glacial erosion as observed by numerous overdeepenings there. When water pressure exceeds ice overburden pressure and flotation is greater than 1, the pattern of subglacial drainages changes to straighter channels that bypass valleys, mountain ranges, and overdeepened basins. This suggests that the maximum potential for glacial erosion by subglacial water channels is obtained when water pressure underneath the Rhine Glacier and Linth Glacier lobes were, on average, close to the ice overburden pressure. These conditions favor high water flow volumes and maximize the potential for subglacial water fluctuations needed for enhanced erosion by ice and water. Finally, comparison of the erosion pattern from subglacial meltwater with those from quarrying and abrasion shows the importance of subglacial water channels in the formation of distal overdeepenings in the Swiss lowlands.